学名;ルーサー 名古屋に発生し現在笹塚に生息する猿種の変種。昭和43年以来1匹しか発見されていないが、人類の言葉を解し人間社会に生きる貴重品。顔面を見る限りでは一見通常の猿だが、「猿」という名称を固有名詞として帰結させるに充分な特殊性を有する。人間を限りない絶望と果てしない感動の世界へと引きずり込むため猿の中の猿として「お猿」という呼び名を与えられるも、人間と接する際は山田佳昌という変名を名乗っているので間違えない様気を付けよう。また笹塚動物園(住居)へ訪れる際は種々の雌を囲っている場合が多いのでこれも気を付けよう。
なお、お猿に接する際には以下の知識が必要である。
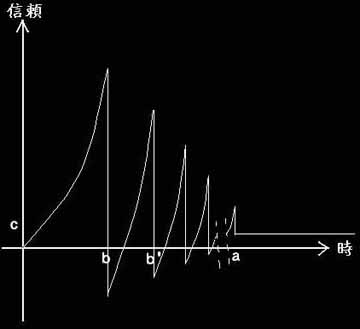
お猿研究室第1回研究発表 「お猿曲線」
縦軸に信頼度、横軸に経過時間を取った、お猿に対する人間の信頼、評価のグラフである。
誰しもがお猿に出会うとその口八丁に乗せられ信頼度は著しく向上する。がある時余りにも綺麗に、美しくその信頼を裏切られ(注:お猿は裏切った等とは認識していない)、信頼度は地に落ちる。しかし再び口八丁により信頼度は向上、そして転落、これを繰り返し何時しか信頼0に収束していく。
研究発表にあたり、クラフの構成要素の詳細をひとつひとつ見てみよう。
お猿曲線 y=f(x)
1)すべて悟り諦めの境地に達すると以降、信頼度は一定する。
y=c(x>a) 「このa点を認容点と称する」
2)極めて長期のスパンで見る限りお猿との接触は利と見ることが可能である。
3)問題となるのは多くの人々は
y<bの時点でお猿との接触をストップ(もしくはb点に至る時間が極めて長い)してしまうことである。残念ながらb点を超えない限り、お猿の本質的理解には決して至らない。
この観点から 「このb点を限界向上点と称する」
4)しかし逆にb点をもってしてお猿に愛想を尽かしてしまっても勿体ない。前述の通りお猿の背信行為を決してお猿自身は認識していない。お猿はその場その場で相対する相手には常に誠心誠意である。ただ直後にそのすべてを忘れてしまうだけなのだ。(「お猿の時空的分断法則」)。よって現在の誠心誠意を後(直後を含む)に期待してはいけないが、現在だけなら持てる能力のすべてを発揮してくれるためお徳用である。
5)なお、このグラフは可成りお猿に好意的に書いてあり、実際は
f(x)=d (y=f'(x)=f(x)−d) (0<d<c)
であり、詰まる所
結局、a点を超えるのが早ければ早いほど、利(S)は大となるのだ。
|
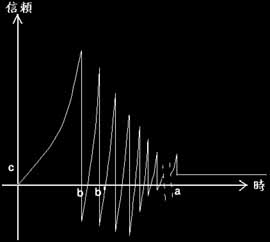
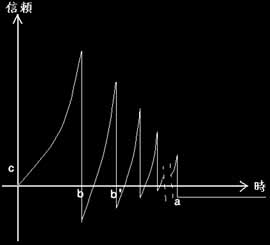
次に、お猿曲線の類型を2つ程挙げよう。 お猿第2曲線(信頼願望系) 左図y=g(x)、これはy=f(x)に比べb点(限界向上点=第一失望点)からb’点(第二失望点)までが短くかつまた、g(b')>f(b')[最大値・最低値ともに]である。 つまり早く大きく信頼度を回復するが、それ故第二失望点での落胆も激しい。最終的にはy=f(x)と同じy=Cに至るため大差はないが、信じる者は救われぬ、という好例である。 お猿第3曲線(最終的信頼喪失系) 左下図y=h(x)はa点に至るまでの過程はy=f(x)と全く同型だが、振幅収縮を繰り返す内に最終的に信頼度をまったく無くしてしまった類型である。このケースでは残念なことにS<0となり、至るはお猿との交渉断絶である。 お猿運用の失敗例だがこの類型に属する人物は最近では少ない様であり、この事から判明するのは、「猿は育つ」である。 こんなお猿が現在まで人間社会で生き長らえているのは、只の猿だったら常にb点で終了している筈の曲線が結果としたSが正になることで証明される様に、「お猿」だからである。 誰も決してお猿の様に生きたくはないが、お猿の様に生きてみたいのもまた一面であるのだ。 お猿、フォーエバー。 お猿よ永久に。 1990.6 文責;Nazoh.X |